Chapter 2 Bits, Data Types, and Operations
bits
Computer is a binary digital system.
- digital: finite number of symbols
- binary: base 2, 0s and 1s
high voltage: 1; low voltage: 0
signed integers
n bits, distinct values,
The maximal positive 011…1 ()
The minimal: 100..000 ()
negative integers (3 methods):
- sign-magnitude: sign bit, the most significant (MS) bit
- 1’s complement: flip every bit to represent negative numbers (problem: +0 and -0)
- 2’s complement (easy for arithmetic):
Note: ignoring carry out (overflow)
1) How to get the representation of a signed integer? -9
- get the positive version 01001 (9)
- flip → 10110
- +1 → 10111
2) How the get the decimal from binary representation? 11011
- flip → 00100
- +1 → 00101
- get the positive version → +5
- signing → -5
arithmetic operations: ADD, SUBTRACT, Sign Extension
logical operations: AND, OR, NOT
Sign Extension: replicate the sign bit
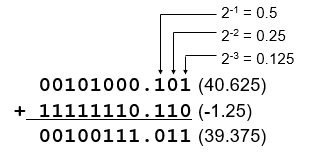
Fractions: fixed-point
- binary point: separate positive from negative powers of two (similar to decimal point)
Floating number
For very large or small numbers.
Scientific notation
1 (Sign) + 8 (Exponent, (exponent - 127)) + 23 (Fraction)
See P47.

Logic operation
XOR: exclusive-OR
| A | B | A XOR B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
DeMorgan’s Laws (relationships between AND and OR)
NOT(NOT(A) AND NOT(B)) = A OR B
NOT(NOT(A) OR NOT(B)) = A AND B
ASCII: American Standard Code for Information Interchange